Designing Electronics that Work Over the last 5 years, I’ve been putting together a 300+ page book with basically everything I learned the hard way over the last 10 years founding and working at several hardware startups. Here’s the Table of Contents: • What to […]
All posts filed under “Uncategorized”

A 60 GHz phased array for $10
A 60 GHz phased array for $10 In 2018, I gave an talk at Hackaday Supercon that was basically Phased Arrays 101. You can watch it at the bottom of this post. At the end of this talk, I mentioned that I was looking for […]

How I won 4 Twitter contests a day (every day for 9 months straight)
How I won 4 Twitter contests a day (every day for 9 months straight) This is the story of how I wrote a Twitter bot to automatically enter contests and ended up winning on average 4 contests per day, every day, for about 9 months straight. […]

Impact – Prevent brain damage in atheletes
Impact – Prevent brain damage in atheletes Note: This project is my entry into the 2015 Hackaday prize and is also documented at Hackaday.io. Millions of young athletes get concussions each year and 50% go undiagnosed, leading to brain […]

Level – A small, frequency agile radio module
Level – A small, frequency agile radio module In the summer of 2012, I started a company with some other Georgia Tech students called Level RF. We went through Y Combinator and lots of really cool and interesting things happened, which you should ask me about sometime. […]

Manhattan Circuits
Manhattan Circuits One really neat method of building circuits without making a PCB is called Manhattan style, so called because the components look like buildings in Manhattan. I really like it because it’s simple, quick, and if you do it right, can be good enough […]

Autolacing Back to the Future shoes
Autolacing Back to the Future shoes In Back to the Future 2, we were promised autolacing shoes by 2015. I figured I’d do my part and help make it happen. This video gives a quick demonstration: And this video goes over it in more […]

Visualizing the emotions of a city
Visualizing the emotions of a city This is a quick project I did over the course of a night or two using some parts I had laying around and had been looking for an excuse to use. An Arduino connects to the internet with an […]
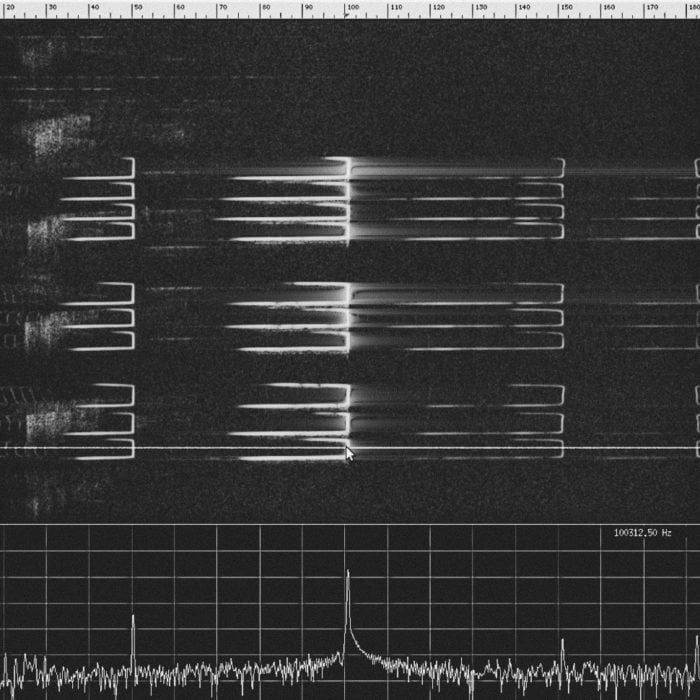
The DSP Behind Bat Echolocation
The DSP Behind Bat Echolocation A couple weeks ago, Dr. Bruce Patterson (the curator of mammals at The Field Museum in Chicago) was kind enough to send me some very high quality recordings of bat vocalizations captured during his recent expedition to Kenya. Bats use a […]

DRFM Radar Jammer
DRFM Radar Jammer This was my senior design project. I worked with two other guys on this and we built a simple, toy DRFM jammer demonstration platform. It uses a USRP as the jammer and the MIT coffee can radar. Here are some pretty pictures: […]

Breathalyzer
Breathalyzer Overview: This is a small project I did over the course of about two months of on and off work while in school. My friend was turning 21, so this was my gift to her. I designed the schematic in a couple of hours […]

Analyzing Trinitite: A (Radioactive) Piece of Nuclear History
Analyzing Trinitite: A (Radioactive) Piece of Nuclear History On July 16, 1945, the United States became the first country to successfully detonate an atomic weapon, signalling the beginning of a new era in warfare and in politics. This detonation took place in the middle of the […]

Machinist’s Cube
Machinist’s Cube The Machinist’s Cube is an old exercise that machinists would do to learn how to mill. The story I’ve always heard is that students would be given a completed cube and asked to replicate it with no further instructions. I did mine on […]

How not to make giant gummy bears
How not to make giant gummy bears I once tried to make a giant gummy bear by melting down smaller gummy bears and pouring them into a mold. It did not go well. I started by melting down some gummy bears. I wanted to use […]

Autonomous Soccer Playing Robots
Autonomous Soccer Playing Robots In college, I was on the Georgia Tech Robocup team in the Small Size league. I worked on the electronics team where I helped build a fleet of robots that autonomously play soccer. Here’s what they look like: Normally, colored circles of paper go in those […]

Could the ancient Romans have built a digital computer?
Could the ancient Romans have built a digital computer? The Romans were undoubtedly master engineers. They were experts at civil engineering, building roads, improving sanitation, inventing Roman concrete, and constructing aqueducts that adhere to tolerances impressive even by today’s standards. Perhaps the best evidence of their aptitude is […]

How to build a pair of $15,000 sensor gloves for $40
How to build a pair of $15,000 sensor gloves for $40 I was working on the Darpa Virtual Robotics Challenge this summer and thought it would be really cool if we could teleop the robot’s grip with some kind of Waldo rig, like they used to control […]
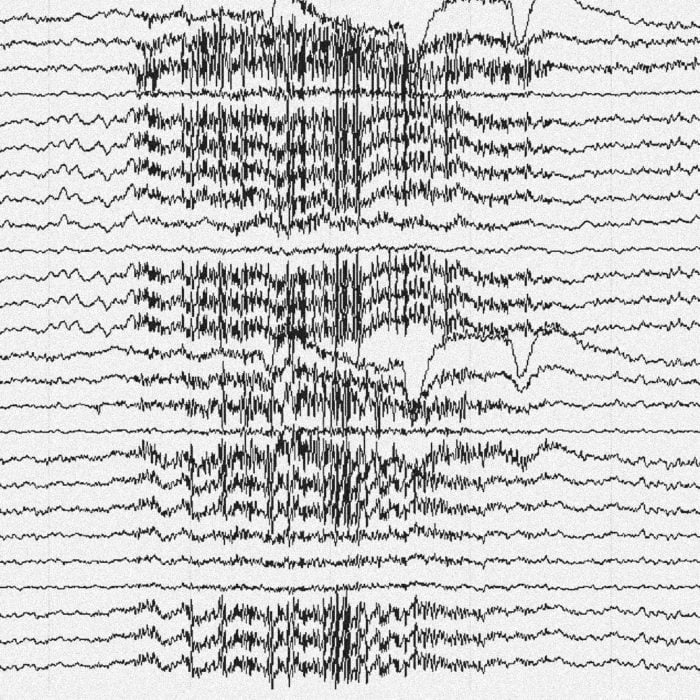
Composing Music with Brainwaves
Composing Music with Brainwaves Introduction This is a project I did for Yahoo HackU 2010. They come to Georgia Tech every year, and I thought it would be fun to compete. I remembered seeing the Star Wars Force Trainer when it came out and I […]

Hack Rifle
Hack Rifle Since some people are concerned: this isn’t a real gun, it’s an airsoft rifle. And yes, pointing anything that looks like a gun at a person or building is a terrible idea, and yes this thing will freak people out and probably get […]

Remote Controlled Can of Soup
A couple years ago, there was a commercial that ran for Chef Boyardee that had a can of soup following a little girl home. You can see it here: This didn’t really mean anything until I was looking around the m5 Industries website. M5 is […]

Wait or Walk
Wait or Walk I built a little web app over Spring Break called Wait or Walk. The bus stops at Georgia Tech tell you how long it is until the next bus, but I realized one day that you don’t really care about that information. […]

Peregrine – An Open Source Flight Computer
Peregrine – An Open Source Flight Computer Dylan Rudolph and I got an open source hardware grant from the good people at Wyolum. They gave us some money to develop a new open source hardware flight computer. The Ardupilot was basically the only hobbiest grade […]

Internet Controlled PowerWheels Rover
Internet Controlled PowerWheels Rover Several summers ago, I and two friends started work on a large, web controlled robot. I had seen people use hardware from Phidgets to control little R/C cars, but Phidgets was too expensive and didn’t give me a fine level of […]
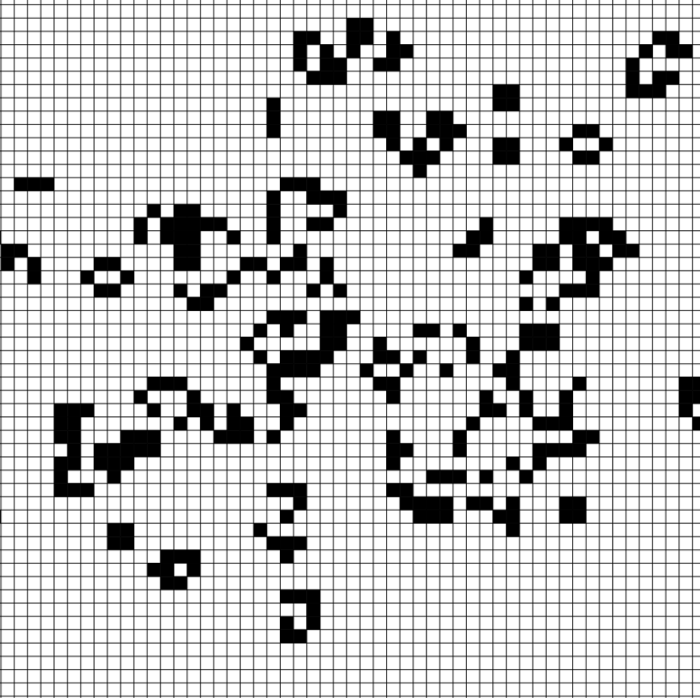
Your Game of Life
Your Game of Life John Conway made up the rules for the game of life by fiddling around until it looked good. Why not make your own game of life and change the rules? Your Game of Life For the unfamiliar, Conway’s Game of Life is […]

USLI Rocket Launch
USLI Rocket Launch I did research on the USLI team developing avionics and a magnetically levitated experiment platform. Here was our first test launch: If you’d like to read more about the technical details behind this rocket, here’s the Flight Readiness Review (FRR). Warning: it’s almost 200 […]

VLSI datapath
VLSI datapath I took a VLSI class this semester and we did a lot of layouts in Virtuoso. Our last lab was making an entire 32 bit datapath. I laid out everything by hand except the control unit at the bottom, which I synthesized. This […]
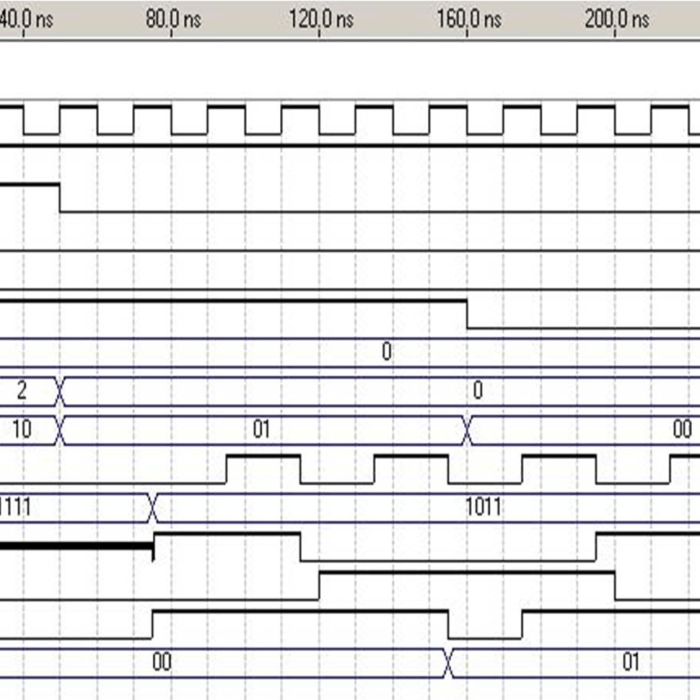
Processor Optimization
Processor Optimization I implemented a processor in VHDL and then pipelined it, adding handling for branch hazards and forwarding. This write up assumes knowledge of how pipelining and forwarding and branch prediction and stuff works. It would take too long to explain all of that […]

Finding the Yellow Line
Finding the Yellow Line This was a project I did a while back, but it’s cool, and I haven’t written about it yet. Recently, several car manufacturers have started including a warning system to yell at you if you start drifting out of your lane. […]

Linux Cluster
Linux Cluster Me and a friend built this my senior year in high school. It’s based on OpenMosix. The grand total spent for this project was $25 (for a 25 port ethernet switch). All of the computers were got for free from either our school […]

Halo Mod
Halo Mod I think I did this while I was a freshman in high school, I can’t really remember. I bought Halo for PC, and Bungee was nice enough to release Halo CE, which allowed for people to make their own maps, weapons, etc. So […]

The importance of packaging
The importance of packaging Software companies spend tremendous time and money on fine tuning the landing page of their app or website because it’s the first thing users see and interact with. You only get one first impression, and users will decide how they feel about […]
Let’s Watch YouTube
Let’s Watch YouTube Let’s Watch YouTube was a project I did as I was learning javascript. It is completely client side, and is my idea of how YouTube should work when you’re trying to watch it with several people. This XKCD comic basically sums up […]
